Advertisements
Advertisements
Question
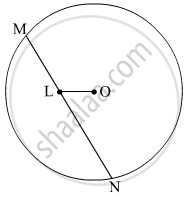
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Solution
seg MN is a chord of a circle with centre O.
Draw OP ⊥ MN and join OM.

MP = PN = `(MN)/2 = 25/2`units (Perpendicular drawn from the centre of a circle on its chord bisects the chord)
∴ LP = MP − ML = `25/2-9=7/2`units
In right ∆OPL,
\[{OL}^2 = {LP}^2 + {OP}^2 \]
\[ \Rightarrow OP = \sqrt{{OL}^2 - {LP}^2}\]
\[ \Rightarrow OP = \sqrt{5^2 - \left( \frac{7}{2} \right)^2}\]
\[ \Rightarrow OP = \sqrt{25 - \frac{49}{4}}\]
\[ \Rightarrow OP = \sqrt{\frac{51}{4}} = \frac{1}{2}\sqrt{51} \] units
In right ∆OPM,
\[{OM}^2 = {MP}^2 + {OP}^2 \]
\[ \Rightarrow OM = \sqrt{\left( \frac{25}{2} \right)^2 + \left( \frac{\sqrt{51}}{2} \right)^2}\]
\[ \Rightarrow OM = \sqrt{\frac{625 + 51}{4}}\]
\[ \Rightarrow OM = \sqrt{\frac{676}{4}}\]
\[ \Rightarrow OM = \sqrt{169} = 13 \] units
Thus, the radius of the circle is 13 units.
APPEARS IN
RELATED QUESTIONS
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
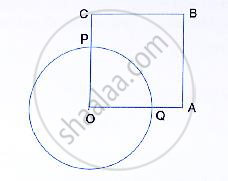
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
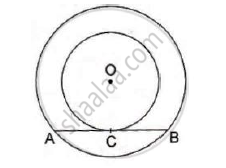
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
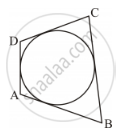
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
In the given figure, O is the centre of the circle. Find ∠CBD.

One chord of a circle is known to be 10 cm. The radius of this circle must be
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
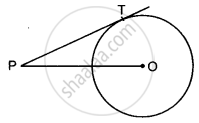
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
The length of tangent from an external point on a circle is always greater than the radius of the circle.
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
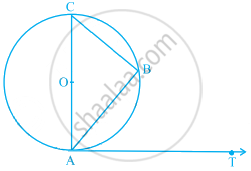
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
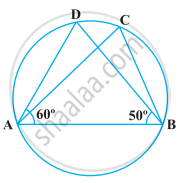
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
Say true or false:
Two diameters of a circle will necessarily intersect.
