Advertisements
Advertisements
Question
In the given figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD.
Complete the following proof by filling in the blanks.
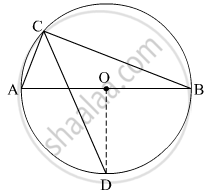
Proof: Draw seg OD.
∠ACB = ______ ...(Angle inscribed in semicircle)
∠DCB = ______ ...(CD is the bisector of ∠C)
m(arc DB) = ______ ...(Inscribed angle theorem)
∠DOB = ______ ...(Definition of measure of an arc)(I)
seg OA ≅ seg OB ...( ____________ )(II)
∴ line OD is ______ of seg AB. ...[From (I) and (II)]
∴ seg AD ≅ seg BD.
Solution
Given: Seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D.
To Prove: seg AD ≅ seg BD.

Proof: Draw seg OD.
∠ACB = 90° ...(Angle inscribed in semicircle)
∠DCB = 45° ...(CD is the bisector of ∠C)
m(arc DB) = 2∠DCB = 90° ...(Inscribed angle theorem)
∠DOB = 90° ...(Definition of measure of an arc)(I)
seg OA ≅ seg OB ...( Radii of the circle )(II)
∴ line OD is perpendicular bisector of seg AB. ...[From (I) and (II)]
∴ seg AD ≅ seg BD
