Advertisements
Advertisements
Question
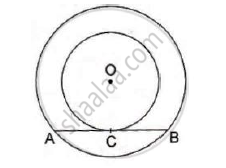
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
Solution
Construction: Join OA, OC and OB

We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OCA = ∠OCB = 90°
Now, In Δ OCA and ΔOCB
∠OCA = ∠OCB = 90°
OA = OB (Radii of the larger circle)
OC = OC (Common)
By RHS congruency
Δ OCA ≅ Δ OCB
∴ CA =CB
RELATED QUESTIONS
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
The circle which passes through all the vertices of a triangle is called ______.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is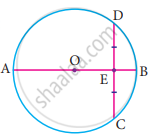
The ratio between the circumference and diameter of any circle is _______
Twice the radius is ________________
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.