Advertisements
Advertisements
Question
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Solution
AB = 10 cm,
BC = 8 cm and
AC = 6 cm
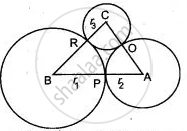
Let the radii of three circle be r1, r2 and r3 ...(Shown in fig.)
r1 + r2 = 10 = AB ....(1)
r2 + r3 = 6 = AC ....(2)
r3 + r1 = 8 = BC .....(3)
Adding (1), (2) and (3), we get
2 (r1 + r2 + r3 ) = 10 + 6 + 8 = 24
r1 + r2 + r3 = 12 .....(4)
Subtract (4) and (1) ⇒ r3 = 12 - 10 = 2 cm
Subtract (4) and (2) ⇒ r1 = 12 - 6 = 6 cm
Subtract (4) and (3) ⇒ r2 = 12 - 8 = 4 cm
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
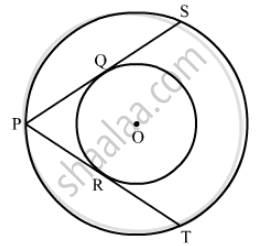
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
The ______________ is the longest chord of a circle
Find the diameter of the circle
Radius = 10 cm
Find the radius of the circle
Diameter = 30 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

From the figure, identify three radii.