Advertisements
Advertisements
Question
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
Solution
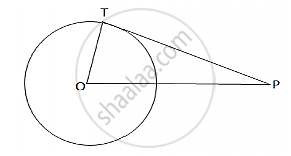
Draw a circle and let P be a point such that OP = 25cm.
Let TP be the tangent, so that TP = 24cm
Join OT where OT is radius.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴ OT ⊥ PT
In the right Δ OTP,we have:
`OP^2 = OT^2 +TP^2 ` [By Pythagoras’ theorem:]
`OT^2 = sqrt(OP^2 - TP^2 )`
`=sqrt(25^2 - 24^2`
`= sqrt(625-576)`
`=sqrt(49)`
= 7 cm
∴ The length of the radius is 7cm.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

If O is the centre of the circle, find the value of x in each of the following figures
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?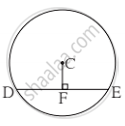
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
Say true or false:
Two diameters of a circle will necessarily intersect.
