Advertisements
Advertisements
Question
If O is the centre of the circle, find the value of x in each of the following figures
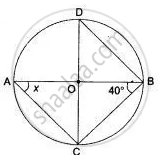
Solution
In BOC,
OB = OC ...(radii)
So, OCB = OBC = 40°
In BOC,
BOC = 180° - (40° + 40°)
BOC = 180° - 80°
So,
x = `"BOC"/2`
x = `(100°)/2` = 50°.
APPEARS IN
RELATED QUESTIONS
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

A line segment joining any point on the circle to its center is called the _____________ of the circle
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
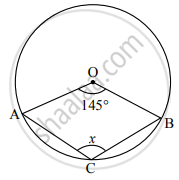
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.