Advertisements
Advertisements
Question
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
Solution
Given ΔABC is isosceles AB = AC
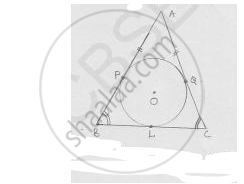
We know that
The tangents from external point to circle are equal in length
From point A, AP = AQ
But AB = AC ⇒ AP + PB = AQ + QC
⇒ PB = PC …. (i)
From B, PB = BL; ….(ii) from C, CL = CQ …..(iii)
From (i), (ii) & (iii)
BL = CL
∴ L bisects BC.
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
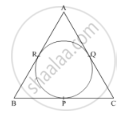
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Draw circle with the radii given below.
2 cm
If O is the center of the circle in the figure alongside, then complete the table from the given information.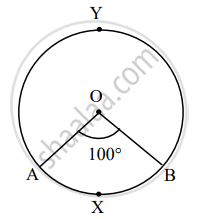
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.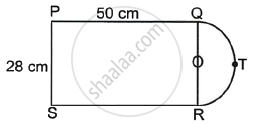
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
