Advertisements
Advertisements
Question
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
Options
A. 34
B. 26
C. 17
D. 14
Solution
Let r1 and r2 be the radii of the two given circles.
Given, 2r1 = 10 cm
∴ r1 = 5 cm
Also, 2r2 = 24 cm
∴ r2 = 12 cm
Let R be the radius of the larger circle.
Given, area of larger circle = Sum of areas of two given circles
`therefore piR^2=pir_1^2+pir_2^2`
`rArr R^2=(5cm)^2+(12cm)^2`
`rArr R^2=25^2+144cm^2`
`rArr R^2=169cm^2`
`rArr R^2=sqrt169cm`
`rArr R^2=13cm`
Thus, the diameter of the larger circle is (2 × 13) cm = 26 cm
Hence, the correct answer is B.
RELATED QUESTIONS
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

Can the length of a chord of a circle be greater than its diameter ? Explain.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
From the figure, identify a diameter.
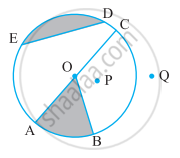
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.