Advertisements
Advertisements
Question
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

Solution
It is given that ∠BCD = 100° and ∠ABD = 70°
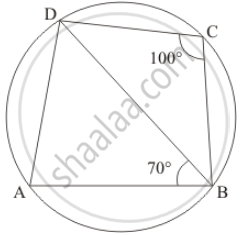
We have to find the ∠ADB
We have
∠A + ∠C = 180° (Opposite pair of angle of cyclic quadrilateral)
So,
`angle A = 180° - 100°`
= 80°
Now in Δ ADB is `angle A ` = 80° and `angle ABD` = 70°
Therefore,
`angle A + angle ADB + angle ABD = 180°`
`80° + angleADB + 70° = 180°`
`angleADB = 180° - 150°`
= 30°
Hence, `angleADB` = 30°
APPEARS IN
RELATED QUESTIONS
In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

Prove that two different circles cannot intersect each other at more than two points.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
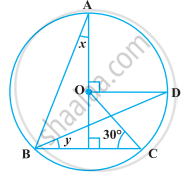
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
