Advertisements
Advertisements
Question
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

Solution
We know that tangent segments to a circle from the same external point are congruent
Now, we have
DS = DR, AR = AQ
Now AD = 23 cm
⇒ AR + RD = 23
⇒ AR =23- RD
⇒ AR = 23 -5 [ ∴ DS = DR = 5]
⇒ AR = 18 CM
Again , AB= 29 cm
⇒ AQ +QB = 29
⇒ QB = 29-AQ
⇒ QB = 29-18 [∵ AR = AQ = 18]
⇒QB = 11CM
Since all the angles are in a quadrilateral BQOP are right angles and OP = BQ
Hence, BQOP is a square.
We know that all the sides of square are equal.
Therefore, BQ = PO = 11 cm
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
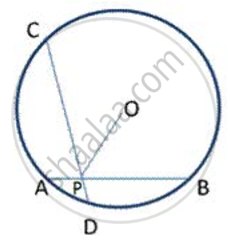
Use the figure given below to fill in the blank:
R is the _______ of the circle.

Use the figure given below to fill in the blank:
EF is a ______ of the circle.

If the radius of a circle is 5 cm, what will its diameter be?
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
