Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

Solution
AB is the chord passing through the center
So, AB is the diameter
Since, angle in a semicircle is a right angle
∴ ∠ APB = 90°
By using alternate segment theorem
We have ∠APB = ∠PAT =30°
Now, in ΔAPB
∠BAP + ∠APB + ∠BAP = 180° (Angle sum property of triangle)
⇒ ∠BAP =180° - 90° -30° = 60°
Now, ∠BAP = ∠APT + ∠PTA (Exterior angle property)
⇒ 60° = 30° +∠PTA
⇒ ∠PTA = 60°- 30°= 30°
We know that sides opposite to equal angles are equal
∴ AP = AT
In right triangle ABP
sin ∠ABP = `(AP)/(BA)`
⇒ sin 30° = `(AT)/(BA)`
⇒ `1/2 =(AT)/(BA)`
∴ BA : AT = 2 :1
RELATED QUESTIONS
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Draw circle with the radii given below.
2 cm
Draw circle with the radii given below.
4 cm
Is every diameter of a circle also a chord?
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
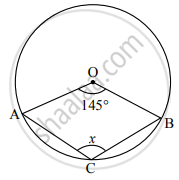
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.