Advertisements
Advertisements
Question
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
Options
60°
45°
30°
15°
Solution
We will associate the given information in the following figure.
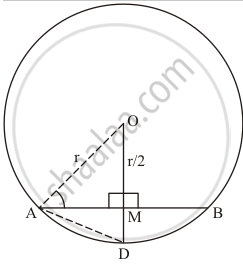
Since AO = r (radius of circle)
AM = `r/2` (given)
Extended OM to D where MD = `r/2`
Consider the triangles AOM and triangle AMD
OM = MD
`angleAMO = angle AMD` = 90°
AM = AM (common Sides
So by SSS property
Δ AMO ≅ Δ DM
So AD = AO = r and OD=OM+MD=r
Hence ΔAOD is equilateral triangle
So `angle OAD` = 60°
We know that in equilateral triangle altitudes divide the vertex angles
Therefore `angleOAM = (angleOAD)/2`
`=60/2`
= 30°
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

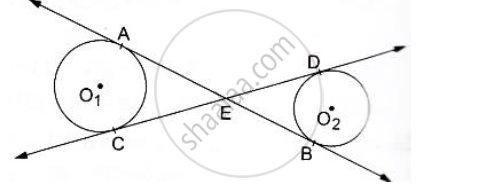
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
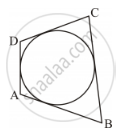
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

The point of concurrence of all angle bisectors of a triangle is called the ______.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
