Advertisements
Advertisements
Question
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
Options
- \[\sqrt{5} \] cm
- \[2\sqrt{5}\] cm
\[2\sqrt{7} \] cm
- \[\sqrt{7}\] cm
Solution
We will represent the given data in the figure
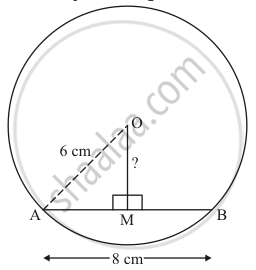
We know that perpendicular drawn from the centre to the chord divides the chord into two equal parts.
So , AM = MB = \[\frac{AB}{2} = \frac{8}{2}\] = 4 cm.
Using Pythagoras theorem in the ΔAMO,
`OM^2 = AO^2 - AM^2`
`= 6^2 - 4^2`
= 36-16
`= sqrt(20)`
= `2sqrt(5)` cm
APPEARS IN
RELATED QUESTIONS
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
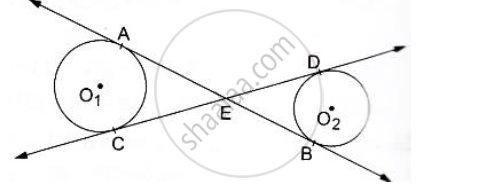
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
A line segment which joins any two points on a circle is a ___________
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
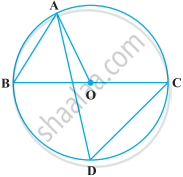
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Is every diameter of a circle also a chord?
