Advertisements
Advertisements
Question
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
Solution
Let O be the centre of the circle and AB be the chord that subtends an angle of 120° at the centre.
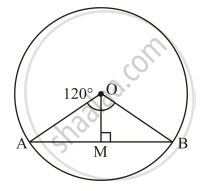
Here, OM ⊥ AB.
Radius of the circle, r = 14 cm
Area of the minor segment = Area of sector OAB − area of ΔAOB
`text{Area of sector OAB}=O/ /360^@ xx pi r^2`
`=120^@/360^@xx22/7xx(14 cm)^2`
`=1/3xx22/7xx196 cm^2`
`=616/3 cm^2`
Now ,OM ⊥ AB.
`∴AM =MB =1/2AB` [Perpendicular from the centre to the bisects the chord]
`rArr AB =2AM `
⇒ AB = 2AM
In ΔOAM and ΔOBM:
OA = OB [Radii of the same circle]
OM = OM [Common]
∠OMA = ∠OMB [Each 90°]
∴ ΔOAM ≅ ΔOBM [RHS congruence criterion]
⇒ ∠AOM = ∠BOM [C.P.C.T]
`∴∠AOM =∠BOM= 120^@/2=60^@`
In ΔAOD:
`rArr sqrt3/2=(AM)/(OA), cos 60^@=(OM)/(OA)`
`rArr sqrt3/2=(AM)/(14 cm),1/2 = (OM)/(14cm)`
`∴ AB=2AM=14sqrt3cm`
`\text{Area} (Δ AOB)=1/2xxABxxOM=1/2xx14sqrt3xx7cm^2=49sqrt3cm^2`
`\text{Area of minor segment}=616/3 cm^2 -49 sqrt3 cm^2`
`=205.33cm^2-49xx1.73cm^2`
`=205.33cm^2-84.77 cm^2`
`=120.56 cm ^2`
Thus, the area of the minor segment is 120.56 cm2.
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
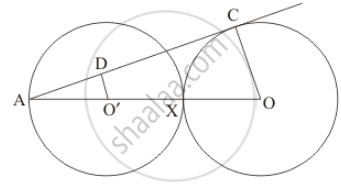
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
Find the radius of the circle
Diameter = 30 cm
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
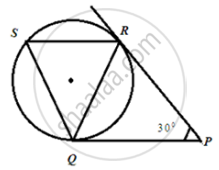
From the figure, identify a sector.

