Advertisements
Advertisements
Question
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are `3/5` times the corresponding sides of the given triangle.
Solution
Construct a right triangle of sides AB = 4 cm, AC = 3 cm and ∠A = 90° and then a triangle similar to it whose sides are `(3/5)^"th"` of the corresponding sides of ΔABC
We follow the following steps to construct the given
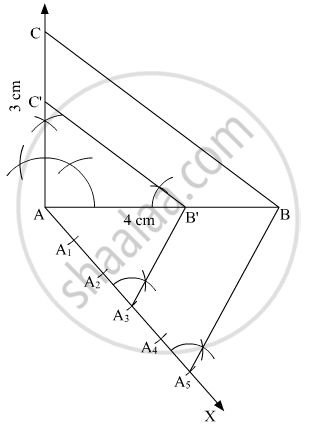
Step of construction
Step: I- First of all we draw a line segment AB = 4 cm.
Step: II- With A as centre and draw an angle ∠A = 90°.
Step: III- With A as centre and radius AC = 3 cm.
Step: IV-Join BC to obtain right ΔABC.
Step: V- Below AB, makes an acute angle ∠BAX.
Step: VI- Along AX, mark off five points A1, A2, A3, A4 and A5 such that =A4A5.
Step: VII- Join A5B.
Step: VIII -Since we have to construct a triangle each of whose sides is (`3/5`)th of the corresponding sides of right ΔABC
So, we draw a line on AX from point which is A3B ∥ A5B and meeting AB at B’.
Step: IX- From B’ point draw B'C' || BCand meeting AC at C’
Thus, ΔABC is the required triangle, each of whose sides is `(3/5)`th of the corresponding sides of ΔABC.
RELATED QUESTIONS
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/2 times the corresponding sides of the isosceles triangle.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
∆ABC ~ ∆LBN. In ∆ABC, AB = 5.1 cm, ∠B = 40°, BC = 4.8 cm, \[\frac{AC}{LN} = \frac{4}{7}\]. Construct ∆ABC and ∆LBN.
Construct ∆PYQ such that, PY = 6.3 cm, YQ = 7.2 cm, PQ = 5.8 cm. If \[\frac{YZ}{YQ} = \frac{6}{5},\] then construct ∆XYZ similar to ∆PYQ.
Find the ratio in which point T(–1, 6)divides the line segment joining the points P(–3, 10) and Q(6, –8).
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3, .... are located at equal distances on the ray AX and the point B is joined to ______.
A triangle ABC is such that BC = 6cm, AB = 4cm and AC = 5cm. For the triangle similar to this triangle with its sides equal to `3/4`th of the corresponding sides of ΔABC, correct figure is?
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
