Advertisements
Advertisements
Question
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/2 times the corresponding sides of the isosceles triangle.
Solution
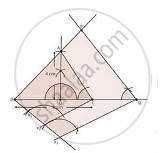
Steps to construct
1. Draw a line segment BC of 8 cm
2. Take a mid point D of BC
3. At D, draw an angler of 90°
4.With centre D,Radius 4cm, draw an arc which intersect line of angle at A
5. Join AB and AC
6. At B, draw an angle CBX of any measure
7. Starting from B, cut there equal parts on BX such that BX1 = X1X2 = X2X3
8. Join X2C
9. Through X3, Draw X3Q || X2C
10. Through Q, Draw QP || CA
∴ ΔPBQ ∼ ΔABC
APPEARS IN
RELATED QUESTIONS
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Construct a ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm. Construct a ΔAQR similar to ΔABC such that side ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are `2/3` times the corresponding sides of ΔABC.
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
Δ AMT ∼ ΔAHE. In Δ AMT, MA = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `(MA)/(HA) = 7/5`. construct Δ AHE.
ΔPQR ~ ΔABC. In ΔPQR, PQ = 3.6cm, QR = 4 cm, PR = 4.2 cm. Ratio of the corresponding sides of triangle is 3 : 4, then construct ΔPQR and ΔABC
A rhombus ABCD in which AB = 4cm and ABC = 60o, divides it into two triangles say, ABC and ADC. Construct the triangle AB’C’ similar to triangle ABC with scale factor `2/3`. Select the correct figure.
If I ask you to construct ΔPQR ~ ΔABC exactly (when we say exactly, we mean the exact relative positions of the triangles) as given in the figure, (Assuming I give you the dimensions of ΔABC and the Scale Factor for ΔPQR) what additional information would you ask for?
A point C divides a line segment AB in the ratio 5 : 6. The ratio of lengths AB: BC is ______.

Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
