Advertisements
Advertisements
प्रश्न
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/2 times the corresponding sides of the isosceles triangle.
उत्तर
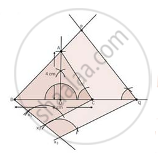
Steps to construct
1. Draw a line segment BC of 8 cm
2. Take a mid point D of BC
3. At D, draw an angler of 90°
4.With centre D,Radius 4cm, draw an arc which intersect line of angle at A
5. Join AB and AC
6. At B, draw an angle CBX of any measure
7. Starting from B, cut there equal parts on BX such that BX1 = X1X2 = X2X3
8. Join X2C
9. Through X3, Draw X3Q || X2C
10. Through Q, Draw QP || CA
∴ ΔPBQ ∼ ΔABC
APPEARS IN
संबंधित प्रश्न
Draw a line segment of length 7 cm and divide it internally in the ratio 2 : 3.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are `3/5` times the corresponding sides of the given triangle.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB) = 3/5 `.
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
Draw seg AB of length 9.7 cm. Take a point P on it such that A-P-B, AP = 3.5 cm. Construct a line MN ⊥ sag AB through point P.
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
To divide a line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the points A1, A2, A3, ... and B1, B2, B3, ... are located at equal distances on ray AX and BY, respectively. Then the points joined are ______.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
Draw a line segment of length 7.5 cm and divide it in the ratio 1:3.
