Advertisements
Advertisements
Question
Construct a ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm. Construct a ΔAQR similar to ΔABC such that side ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
Solution
Given that
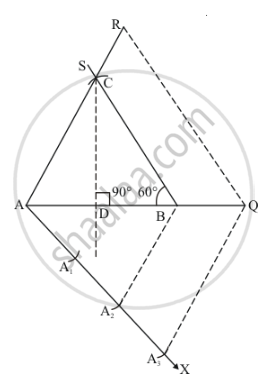
Construct a triangle ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm and then a triangle ΔAQR similar to it whose sides are (1.5 times = 3/2) of the corresponding sides of ΔACB.
We follow the following steps to construct the given
Step of construction
Step: I- First of all we draw a line segment AB = 5cm.
Step: II- With B as centre and draw an angle ∠B = 60°.
Step: III -From point A and B construct altitude CD = 3cm, which cut the line BS at point C
Step: IV- Join AC to obtain ΔABC.
Step: V- Below AB, makes an acute angle ∠BAX = 60°.
Step: VI- Along AX, mark off five points A1, A2 and A3 such that AA1 = A1A2 = A2A3
Step: VII -Join A2B.
Step: VIII -Since we have to construct a triangle ΔAQR each of whose sides is (1.5 times = 3/2) of the corresponding sides of ΔABC.
So, we draw a line A3Q on AX from point A3 which is A3Q||A2B and meeting AB at Q.
Step: IX- From Q point draw QR || BC and meeting AC at R
Thus, ΔAQR is the required triangle, each of whose sides is (1.5 times = 3/2) of the corresponding sides of ΔABC.
APPEARS IN
RELATED QUESTIONS
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are `7/5` of the corresponding sides of the first triangle. Give the justification of the construction.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the first triangle.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are `2/3` times the corresponding sides of ΔABC.
Δ SHR ∼ Δ SVU. In Δ SHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and
SHSV = 53 then draw Δ SVU.
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
To construct a triangle similar to a given ΔABC with its sides `3/7` of the corresponding sides of ΔABC, first draw a ray BX such that ∠CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points B1, B2, B3, ... on BX at equal distances and next step is to join ______.
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
What is the ratio `(AC)/(BC)` for the line segment AB following the construction method below?
Step 1: A ray is extended from A and 30 arcs of equal lengths are cut, cutting the ray at A1, A2,…A30
Step 2: A line is drawn from A30 to B and a line parallel to A30B is drawn, passing through the point A17 and meet AB at C.
Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and ∠B = 90°. Construct a triangle similar to it and of scale factor `2/3`. Is the new triangle also a right triangle?
Draw an isosceles triangle ABC in which AB = AC = 6 cm and BC = 5 cm. Construct a triangle PQR similar to ∆ABC in which PQ = 8 cm. Also justify the construction.
