Question

Construct a ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm. Construct a ΔAQR similar to ΔABC such that side ΔAQR is 1.5 times that of the corresponding sides of ΔACB.

Answer 1

Given that

Construct a triangle ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm and then a triangle ΔAQR similar to it whose sides are (1.5 times = 3/2) of the corresponding sides of ΔACB.

We follow the following steps to construct the given

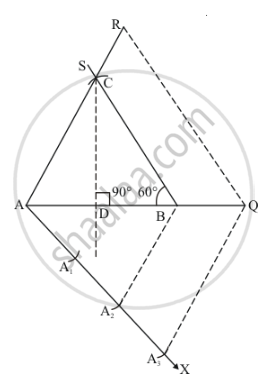
Step of construction

Step: I- First of all we draw a line segment AB = 5cm.

Step: II- With B as centre and draw an angle ∠B = 60°.

Step: III -From point A and B construct altitude CD = 3cm, which cut the line BS at point C

Step: IV- Join AC to obtain ΔABC.

Step: V- Below AB, makes an acute angle ∠BAX = 60°.

Step: VI- Along AX, mark off five points A₁, A₂ and A₃ such that AA₁ = A₁A₂ = A₂A₃

Step: VII -Join A₂B.

Step: VIII -Since we have to construct a triangle ΔAQR each of whose sides is (1.5 times = 3/2) of the corresponding sides of ΔABC.

So, we draw a line A₃Q on AX from point A₃ which is A₃Q||A₂B and meeting AB at Q.

Step: IX- From Q point draw QR || BC and meeting AC at R

Thus, ΔAQR is the required triangle, each of whose sides is (1.5 times = 3/2) of the corresponding sides of ΔABC.