Advertisements
Advertisements
प्रश्न
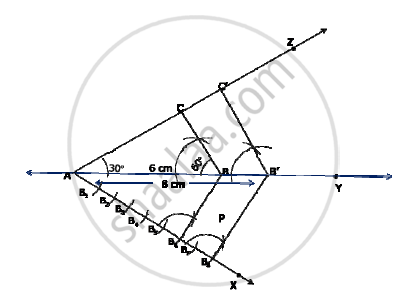
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
उत्तर
Construct the Δ ABC as per given measurements.
1) in the half plane if `bar(AB)` which does not contain C,
2)draw `vec(AX)` such that ∠BAX is an acute angle
3) With some appropriate radius and centre A, Draw an arc to intersect vec(AX) at B_1. Similarly, with center B_1 and same radius, drawn an arc to intersect `vec(BX)` at B2 such that `B_1B_2=B_3B_4=B_4B_5=B_5B_6=B_6B_7=B_7B_8`
4) Draw bar(B6B)
5) Through B8 draw a ray parallel to bar(B6B).to intersect `bar(AY)` at B'.
6) Through B' draw aray parallel to `bar (BC)` to intersect `bar(AZ)` at C' thus , ΔAB'C' is required triangle
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60˚. Now construct another triangle whose sides are 5/7 times the corresponding sides of ΔABC.
Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
Find the co-ordinates of the points of trisection of the line segment AB with A(2, 7) and B(–4, –8).
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
∆ABC ~ ∆PBQ. In ∆ABC, AB = 3 cm, ∠B = 90°, BC = 4 cm. Ratio of the corresponding sides of two triangles is 7 : 4. Then construct ∆ABC and ∆PBQ
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
