Advertisements
Advertisements
प्रश्न
Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60˚. Now construct another triangle whose sides are 5/7 times the corresponding sides of ΔABC.
उत्तर
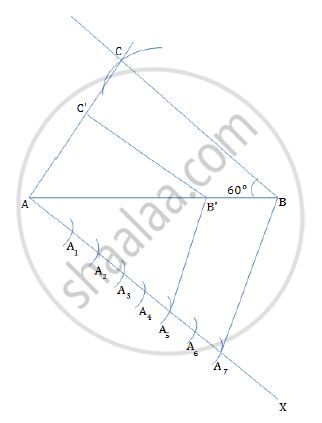
Steps for construction:
1. Draw a line segment AB = 5 cm.
2. At B construct m∠ABC = 60°
3. Take a measure of 6 cm, and draw an arc from B on BC.
4. Join AC to obtain ΔABC.
5. Below AB, make an acute angle ∠BAX.
6. Since 7 > 5, mark off 7 points A1, A2, A3, A4, A5, A6 and A7 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7.
7. Join A7B.
8. Since we have to construct a triangle each of whose sides is 5/7 of the corresponding sides of ABC. So take five parts out of seven equal parts on AX. i.e. from point A5, draw A5B' || A7B, meeting AB at B'.
9. From B', draw B'C' || BC, meeting AC at C'
10.ΔAB'C' is the required, each of the sides is five-seventh of the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are`3/4` times the corresponding sides of ΔABC.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
∆ABC ~ ∆LBN. In ∆ABC, AB = 5.1 cm, ∠B = 40°, BC = 4.8 cm, \[\frac{AC}{LN} = \frac{4}{7}\]. Construct ∆ABC and ∆LBN.
Construct an equilateral ∆ABC with side 5 cm. ∆ABC ~ ∆LMN, ratio the corresponding sides of triangle is 6 : 7, then construct ΔLMN and ΔABC
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
A rhombus ABCD in which AB = 4cm and ABC = 60o, divides it into two triangles say, ABC and ADC. Construct the triangle AB’C’ similar to triangle ABC with scale factor `2/3`. Select the correct figure.
If I ask you to construct ΔPQR ~ ΔABC exactly (when we say exactly, we mean the exact relative positions of the triangles) as given in the figure, (Assuming I give you the dimensions of ΔABC and the Scale Factor for ΔPQR) what additional information would you ask for?
What is the ratio `(AC)/(BC)` for the line segment AB following the construction method below?
Step 1: A ray is extended from A and 30 arcs of equal lengths are cut, cutting the ray at A1, A2,…A30
Step 2: A line is drawn from A30 to B and a line parallel to A30B is drawn, passing through the point A17 and meet AB at C.
What is the ratio `(AC)/(BC)` for the following construction: A line segment AB is drawn. A single ray is extended from A and 12 arcs of equal lengths are cut, cutting the ray at A1, A2… A12.A line is drawn from A12 to B and a line parallel to A12B is drawn, passing through the point A6 and cutting AB at C.
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
