Advertisements
Advertisements
प्रश्न
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
उत्तर
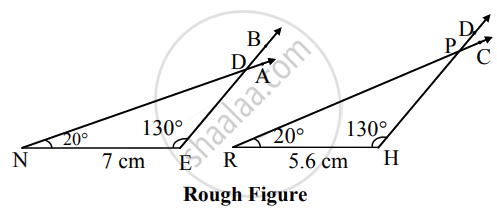
Analysis:
In ∆NED, ∠D = 30° and ∠N = 20° ......[Given]
∴ ∠E = 130° ......(ii) [Remaining angle of a triangle]
∆RHP ∼ ∆NED
∴ `"RH"/"NE" = "HP"/"ED" = "PR"/"DN"` ......[Corresponding sides of similar triangles]
∴ `"RH"/7 = 4/5` ......[Given]
∴ RH = `(4 xx 7)/5` = 5.6 cm
Also, ∠R = ∠N, ∠H = ∠E, ∠P = ∠D ......(iiii) [Corresponding angles of similar triangles]
∴ ∠R = 20°, ∠H = 130°, ∠P = 30° ......[From (i), (ii) and (iii)]

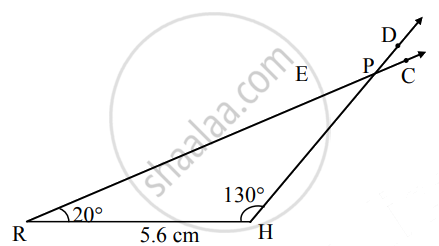
Steps of construction:
| ∆NED | ∆RHP | |
| i. | Draw seg NE of 7 cm | Draw seg RH of 5.6 cm |
| ii. | Draw a ray NA and EB such that ∠ANE = 20° and ∠BEN = 130°. | Draw a ray RC and HD such that ∠CRH = 20° and ∠DHR = 130°. |
| iii. | Name the point of intersection of rays D. | Name the point of intersection of rays P. |
APPEARS IN
संबंधित प्रश्न
Write down the equation of a line whose slope is 3/2 and which passes through point P, where P divides the line segment AB joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are`3/4` times the corresponding sides of ΔABC.
Draw a line segment of length 7 cm and divide it internally in the ratio 2 : 3.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are `3/5` times the corresponding sides of the given triangle.
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3 Also, justify your construction.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also, justify your construction.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are 5/3th times the corresponding sides of the given triangle.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB) = 3/5 `.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are `2/3` times the corresponding sides of ΔABC.
∆PQR ~ ∆LTR. In ∆PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct ∆PQR and ∆LTR, such that `"PQ"/"LT" = 3/4`.
∆AMT ~ ∆AHE. In ∆AMT, AM = 6.3 cm, ∠TAM = 50°, AT = 5.6 cm. `"AM"/"AH" = 7/5`. Construct ∆AHE.
∆ABC ~ ∆LBN. In ∆ABC, AB = 5.1 cm, ∠B = 40°, BC = 4.8 cm, \[\frac{AC}{LN} = \frac{4}{7}\]. Construct ∆ABC and ∆LBN.
If A(–14, –10), B(6, –2) is given, find the coordinates of the points which divide segment AB into four equal parts.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
Find the ratio in which the segment joining the points (1, –3) and (4, 5) is divided by the x-axis? Also, find the coordinates of this point on the x-axis.
Choose the correct alternative:

In the figure ΔABC ~ ΔADE then the ratio of their corresponding sides is ______
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm, ∠D = 30°, ∠N = 20° and `"HP"/"ED" = 4/5`. Then construct ΔRHP and ΔNED
ΔAMT ~ ΔAHE. In ΔAMT, AM = 6.3 cm, ∠MAT = 120°, AT = 4.9 cm, `"AM"/"HA" = 7/5`, then construct ΔAMT and ΔAHE
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn so that ∠BAX is an acute angle and then at equal distances points are marked on the ray AX such that the minimum number of these points is ______.
A triangle ABC is such that BC = 6cm, AB = 4cm and AC = 5cm. For the triangle similar to this triangle with its sides equal to `3/4`th of the corresponding sides of ΔABC, correct figure is?
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
If you need to construct a triangle with point P as one of its vertices, which is the angle that you need to construct a side of the triangle?
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
What is the ratio `(AC)/(BC)` for the following construction: A line segment AB is drawn. A single ray is extended from A and 12 arcs of equal lengths are cut, cutting the ray at A1, A2… A12.A line is drawn from A12 to B and a line parallel to A12B is drawn, passing through the point A6 and cutting AB at C.
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor `5/3`.
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
