Advertisements
Advertisements
प्रश्न
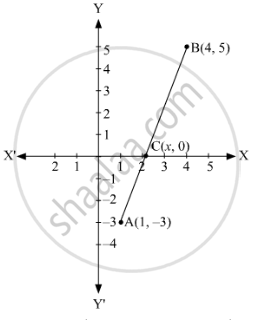
Find the ratio in which the segment joining the points (1, –3) and (4, 5) is divided by the x-axis? Also, find the coordinates of this point on the x-axis.
उत्तर
Let C(x, 0) divides the line-segment A(1, –3) and B(4, 5) in k : 1 ratio.
By section formula,
`(x, y ) = ((mx_2 + nx_1)/(m+n), (my_2 + ny_2)/(m +n))`
⇒ `(x,0) = ((4k + 1xx1)/(k + 1) , (5k + 1 xx (-3))/(k + 1))`
⇒ `(x , 0) = ((4k + 1)/(k + 1) , (5k - 3)/(k + 1))`
⇒ `(5k - 3)/(k + 1) = 0`
⇒ `5k - 3 = 0`
⇒ `5k = 3`
⇒ `k = (3)/(5)`
and `x = (4k + 1)/(k + 1) = (4 xx (3)/(5) +1)/((3)/(5)+1)`
⇒ `x = ((12+5)/(5))/((3+5)/(5))`
⇒ `x = (17)/(8)`
The ratio in which C divides A and B is k : 1 i.e., 3 : 5 and the coordinate of C is `((17)/(8) , 0)`.
संबंधित प्रश्न
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
∆PQR ~ ∆LTR. In ∆PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct ∆PQR and ∆LTR, such that `"PQ"/"LT" = 3/4`.
∆ABC ~ ∆PBQ. In ∆ABC, AB = 3 cm, ∠B = 90°, BC = 4 cm. Ratio of the corresponding sides of two triangles is 7 : 4. Then construct ∆ABC and ∆PBQ
ΔABC ~ ΔPBR, BC = 8 cm, AC = 10 cm , ∠B = 90°, `"BC"/"BR" = 5/4` then construct ∆ABC and ΔPBR
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x - y + 2 = 0, then value of k is ______.
To divide a line segment AB in the ratio p : q (p, q are positive integers), draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is ______.
Match the following based on the construction of similar triangles, if scale factor `(m/n)` is.
| Column I | Column II | ||
| i | >1 | a) | The similar triangle is smaller than the original triangle. |
| ii | <1 | b) | The two triangles are congruent triangles. |
| iii | =1 | c) | The similar triangle is larger than the original triangle. |
The basic principle used in dividing a line segment is ______.
By geometrical construction, it is possible to divide a line segment in the ratio `sqrt(3) : 1/sqrt(3)`.
Draw a line segment AB of length 10 cm and divide it internally in the ratio of 2:5 Justify the division of line segment AB.
