Advertisements
Advertisements
Question
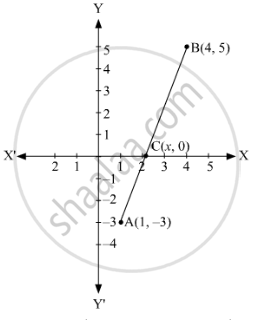
Find the ratio in which the segment joining the points (1, –3) and (4, 5) is divided by the x-axis? Also, find the coordinates of this point on the x-axis.
Solution
Let C(x, 0) divides the line-segment A(1, –3) and B(4, 5) in k : 1 ratio.
By section formula,
`(x, y ) = ((mx_2 + nx_1)/(m+n), (my_2 + ny_2)/(m +n))`
⇒ `(x,0) = ((4k + 1xx1)/(k + 1) , (5k + 1 xx (-3))/(k + 1))`
⇒ `(x , 0) = ((4k + 1)/(k + 1) , (5k - 3)/(k + 1))`
⇒ `(5k - 3)/(k + 1) = 0`
⇒ `5k - 3 = 0`
⇒ `5k = 3`
⇒ `k = (3)/(5)`
and `x = (4k + 1)/(k + 1) = (4 xx (3)/(5) +1)/((3)/(5)+1)`
⇒ `x = ((12+5)/(5))/((3+5)/(5))`
⇒ `x = (17)/(8)`
The ratio in which C divides A and B is k : 1 i.e., 3 : 5 and the coordinate of C is `((17)/(8) , 0)`.
RELATED QUESTIONS
Draw a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then construct another triangle whose sides are\[\frac{3}{5}\] of the corresponding sides of ∆ABC ?
To divide a line segment AB in the ratio 4 : 7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1, A2, A3, .... are located at equal distances on the ray AX and the point B is joined to ______.
By geometrical construction, it is possible to divide a line segment in the ratio ______.
For ∆ABC in which BC = 7.5cm, ∠B =45° and AB - AC = 4, select the correct figure.
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
The basic principle used in dividing a line segment is ______.
To divide a line segment, the ratio of division must be ______.
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor `5/3`.
