Advertisements
Advertisements
प्रश्न
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor `5/3`.
उत्तर
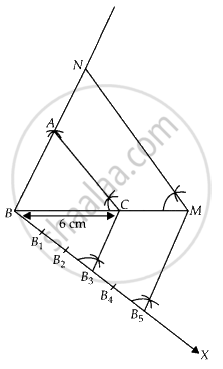
Steps of construction:
- Draw a line segment BC = 6 cm.
- Taking B and C as centres, draw two arcs of radii 4 cm and 5 cm intersecting each other at A.
- Join BA and CA. ∆ABC is the required triangle.
- From B, draw any ray BX downwards making at acute angle.
- Mark five points B1, B2, B3, B4 and B5 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
- Join B3C and from B5 draw B5M || B3C intersecting the extended line segment BC at M.
- From point M draw MN || CA intersecting the extended line segment BA at N.
Then, ∆NBM is the required triangle whose sides is equal to `5/3` of the corresponding sides of the ∆ABC.
Hence, ∆NBM is the required triangle.
APPEARS IN
संबंधित प्रश्न
Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are `2/3` of the corresponding sides of the first triangle. Give the justification of the construction.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the first triangle.
Find the ratio in which point T(–1, 6)divides the line segment joining the points P(–3, 10) and Q(6, –8).
Given A(4, –3), B(8, 5). Find the coordinates of the point that divides segment AB in the ratio 3 : 1.
∆ABC ~ ∆PBQ. In ∆ABC, AB = 3 cm, ∠B = 90°, BC = 4 cm. Ratio of the corresponding sides of two triangles is 7 : 4. Then construct ∆ABC and ∆PBQ
If the point P (6, 7) divides the segment joining A(8, 9) and B(1, 2) in some ratio, find that ratio
Solution:
Point P divides segment AB in the ratio m: n.
A(8, 9) = (x1, y1), B(1, 2 ) = (x2, y2) and P(6, 7) = (x, y)
Using Section formula of internal division,
∴ 7 = `("m"(square) - "n"(9))/("m" + "n")`
∴ 7m + 7n = `square` + 9n
∴ 7m – `square` = 9n – `square`
∴ `square` = 2n
∴ `"m"/"n" = square`
For ∆ABC in which BC = 7.5cm, ∠B =45° and AB - AC = 4, select the correct figure.
When a line segment is divided in the ratio 2 : 3, how many parts is it divided into?
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
