Advertisements
Advertisements
प्रश्न
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the first triangle.
उत्तर
Given that
Construct a right triangle of sides let AB = 8cm, AC = 6cm and ∠ A = 90° and then a triangle similar to it whose sides are 3/4th of the corresponding sides of ΔABC.
We follow the following steps to construct the given
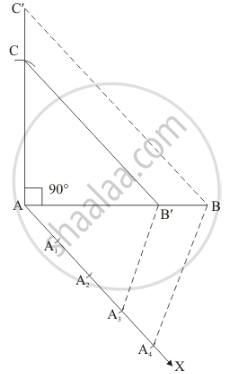
Step of construction
Step: I- First of all we draw a line segment let AB = 8cm.
Step: II- With A as centre and draw an angle ∠ A = 90°.
Step: III- With A as centre and radius AC = 6cm.
Step: IV-Join BC to obtain right ΔABC.
Step: V- Below AB, makes an acute angle ∠BAX = 60°.
Step: VI- Along AX, mark off five points A1, A2, A3 and A4 such that AA1 = A1A2 = A2A3 = A3A4
Step: VII- Join A4B.
Step: VIII -Since we have to construct a triangle each of whose sides is 3/4th of the corresponding sides of right ΔABC.
So, we draw a line A3B' on AX from point A3 which is A3B' || A4B, and meeting AB at B’.
Step: IX- From B’ point draw B'C || BC and meeting AC at C’
Thus, ΔAB'C' is the required triangle, each of whose sides is 3/4th of the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts. Give the justification of the construction.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are `7/5` of the corresponding sides of the first triangle. Give the justification of the construction.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/2 times the corresponding sides of the isosceles triangle.
If A (20, 10), B(0, 20) are given, find the coordinates of the points which divide segment AB into five congruent parts.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that `(AP)/(AB)=3/5`.
Draw a right triangle in which the sides (other than the hypotenuse) are of lengths 4 cm and 3 cm. Now construct another triangle whose sides are \[\frac{3}{5}\] times the corresponding sides of the given triangle.
ΔRHP ~ ΔNED, In ΔNED, NE = 7 cm. ∠D = 30°, ∠N = 20°, `"HP"/"ED" = 4/5`, then construct ΔRHP and ∆NED
If I ask you to construct ΔPQR ~ ΔABC exactly (when we say exactly, we mean the exact relative positions of the triangles) as given in the figure, (Assuming I give you the dimensions of ΔABC and the Scale Factor for ΔPQR) what additional information would you ask for?
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5.
