Advertisements
Advertisements
प्रश्न
Draw a triangle ABC in which BC = 6 cm, CA = 5 cm and AB = 4 cm. Construct a triangle similar to it and of scale factor `5/3`.
उत्तर
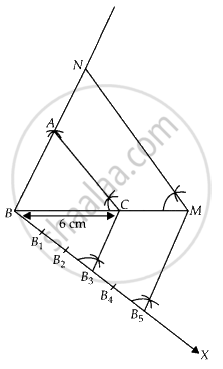
Steps of construction:
- Draw a line segment BC = 6 cm.
- Taking B and C as centres, draw two arcs of radii 4 cm and 5 cm intersecting each other at A.
- Join BA and CA. ∆ABC is the required triangle.
- From B, draw any ray BX downwards making at acute angle.
- Mark five points B1, B2, B3, B4 and B5 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
- Join B3C and from B5 draw B5M || B3C intersecting the extended line segment BC at M.
- From point M draw MN || CA intersecting the extended line segment BA at N.
Then, ∆NBM is the required triangle whose sides is equal to `5/3` of the corresponding sides of the ∆ABC.
Hence, ∆NBM is the required triangle.
APPEARS IN
संबंधित प्रश्न
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose side are `1 1/2` times the corresponding sides of the isosceles triangle.
Give the justification of the construction
Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)th of the corresponding sides of Δ ABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm, ∠A = 60° with scale factor 4 : 5.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are 3/4 times the corresponding sides of the first triangle.
Construct the circumcircle and incircle of an equilateral ∆XYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Construct ∆PYQ such that, PY = 6.3 cm, YQ = 7.2 cm, PQ = 5.8 cm. If \[\frac{YZ}{YQ} = \frac{6}{5},\] then construct ∆XYZ similar to ∆PYQ.
Find the ratio in which point P(k, 7) divides the segment joining A(8, 9) and B(1, 2). Also find k.
Find the co-ordinates of the centroid of the Δ PQR, whose vertices are P(3, –5), Q(4, 3) and R(11, –4)
A point C divides a line segment AB in the ratio 5 : 6. The ratio of lengths AB: BC is ______.

What is the ratio `(AC)/(BC)` for the line segment AB following the construction method below?
Step 1: A ray is extended from A and 30 arcs of equal lengths are cut, cutting the ray at A1, A2,…A30
Step 2: A line is drawn from A30 to B and a line parallel to A30B is drawn, passing through the point A17 and meet AB at C.
