Advertisements
Advertisements
प्रश्न
Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)th of the corresponding sides of Δ ABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
उत्तर
Given that
AB = 5 cm, BC = 7 cm and ∠ABC = 50°
Construct a triangle similar to a triangle ABC such that each of sides is (5/7)th of the corresponding sides of triangle ABC.
We follow the following steps to construct the given
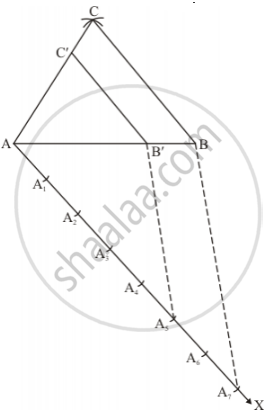
Step of construction
Step: I- First of all we draw a line segment AB = 5 cm.
Step: II- With B as centre and draw an angle ∠ABY = 50°.
Step: III- With B as centre and radius = BC = 7 cm, draw an arc, cut the line BY drawn in step II at C.
Step: IV- Joins AC to obtain ΔABC.
Step: V- Below AB, makes an acute angle ∠BAX = 60°.
Step: VI- Along AX, mark off seven points A1, A2, A3, A4, A5, A6 and A7 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7
Step: VII-Join A7B.
Step: VIII- Since we have to construct a triangle each of whose sides is (5/7)th of the corresponding sides of ΔABC.
So, we take five parts out of seven equal parts on AX from point A5 draw A5B' || A7B and meeting AB at B’.
Step: IX- From B'draw B'C || BC and meeting AC at C’
Thus, ΔAB'C' is the required triangle, each of whose sides is (5/7)th of the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts. Give the justification of the construction.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. the construct another triangle whose sides are `5/3` times the corresponding sides of the given triangle. Give the justification of the construction.
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are `3/5` times the corresponding sides of the given triangle.
To divide a line segment AB in the ratio p : q (p, q are positive integers), draw a ray AX so that ∠BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is ______.
If the perpendicular distance between AP is given, which vertices of the similar triangle would you find first?
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The basic principle used in dividing a line segment is ______.
To construct a triangle similar to a given ∆ABC with its sides `7/3` of the corresponding sides of ∆ABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect to BC. The points B1, B2, ...., B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C where C' lies on BC produced. Finally, line segment A'C' is drawn parallel to AC.
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor `3/2`. Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.
