Advertisements
Advertisements
प्रश्न
Construct a triangle similar to a given ΔABC such that each of its sides is (2/3)rd of the corresponding sides of ΔABC. It is given that BC = 6 cm, ∠B = 50° and ∠C = 60°.
उत्तर
Given that
Construct a triangle of given data, BC = 6 cm, ∠B = 50° and ∠C = 60° and then a triangle similar to it whose sides are (2/3)rd of the corresponding sides of ΔABC.
We follow the following steps to construct the given
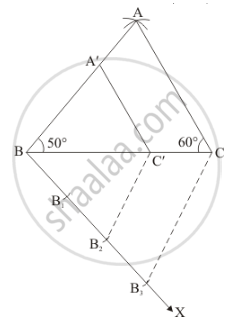
Step of construction
Step: I- First of all we draw a line segment Bc = 60°.
Step: II- With B as centre draw an angle ∠B = 50°.
Step: III- With C as centre draw an angle ∠C = 60° which intersecting the line drawn in step II at A.
Step: IV- Joins AB and AC to obtain ΔABC.
Step: V -Below BC, makes an acute angle ∠CBX = 60°.
Step: VI -Along BX, mark off three points B1, B2 and B3 such that BB1 = B1B2 = B2B3
Step: VII -Join B3C.
Step: VIII -Since we have to construct a triangle each of whose sides is two-third of the corresponding sides of ΔABC.
So, we take two parts out of three equal parts on BX from point B2 draw B2C' || B3C, and meeting BC at C’.
Step: IX -From C’ draw C'A' || AC and meeting AB at A’
Thus, ΔA'BC' is the required triangle, each of whose sides is two third of the corresponding sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
Construct a triangle ABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ∆ABC.
Construct a ΔABC in which AB = 5 cm. ∠B = 60° altitude CD = 3cm. Construct a ΔAQR similar to ΔABC such that side ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
Given A(4, –3), B(8, 5). Find the coordinates of the point that divides segment AB in the ratio 3 : 1.
Choose the correct alternative:
______ number of tangents can be drawn to a circle from the point on the circle.
To construct a triangle similar to a given ΔABC with its sides `8/5` of the corresponding sides of ΔABC draw a ray BX such that ∠CBX is an acute angle and X is on the opposite side of A with respect to BC. Then minimum number of points to be located at equal distances on ray BX is ______.
If a triangle similar to given ΔABC with sides equal to `3/4` of the sides of ΔABC is to be constructed, then the number of points to be marked on ray BX is ______.

The point W divides the line XY in the ratio m : n. Then, the ratio of lengths of the line segments XY : WX is ______.
What is the ratio `(AC)/(BC)` for the line segment AB following the construction method below?
Step 1: A ray is extended from A and 30 arcs of equal lengths are cut, cutting the ray at A1, A2,…A30
Step 2: A line is drawn from A30 to B and a line parallel to A30B is drawn, passing through the point A17 and meet AB at C.
Two line segments AB and AC include an angle of 60° where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively such that AP = `3/4` AB and AQ = `1/4` AC. Join P and Q and measure the length PQ.
Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?
