Question

Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm and ∠ABC = 60°, divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD' C' similar to ∆BDC with scale factor `4/3`. Draw the line segment D'A' parallel to DA where A' lies on extended side BA. Is A'BC'D' a parallelogram?

Answer 1

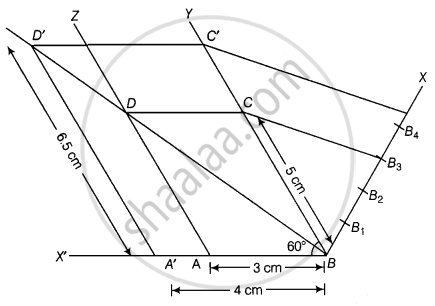
Steps of construction

1. Draw a line segment AB = 3 cm.
2. Now, draw a ray BY making an acute ∠ABY = 60°.
3. With B as centre and radius equal to 5 cm draw an arc cut the point C on BY.
4. Again draw a ray AZ making an acute ∠ZAX’ = 60°.  ...[∴ BY || AZ, ∴ ∠YBX’ = ZAX’ = 60°]
5. With A as centre and radius equal to 5 cm draw an arc cut the point D on AZ.
6. Now, join CD and finally make a parallelogram ABCD.
7. Join BD, which is a diagonal of parallelogram ABCD.
8. From B draw any ray BX downwards making an acute ∠CBX.
9. Locate 4 points B₁, B₂, B₃, B₄ on BX, such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
10. Join B₄C and from B₃C draw a line B₄C’ || B₃C intersecting the extended line segment BC at C’.
11. From point C’ draw C’D’ || CD intersecting the extended line segment BD at D’. Then, AD’BC’ is the required triangle whose sides are `4/3` of the corresponding sides of ΔDBC.
12. Now draw a line segment D’A’ parallel to DA, where A’ lies on extended side BA i.e., ray BX’.
13. Finally, we observe that A’BCD’ is a parallelogram in which A’D’ = 6.5 cm A’B = 4 cm and ∠A’BD’ = 60° divide it into triangles BC'D’ and A’BD’ by the diagonal BD.