Advertisements
Advertisements
प्रश्न
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
उत्तर
Given, two concentric circles of radii 3 cm and 5 cm with centre O. We have to draw pair of tangents from point P on outer circle to the other.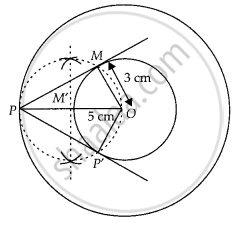
Steps of construction:
- Draw two concentric circles with centre O and radii 3 cm and 5 cm.
- Taking any point P on outer circle. Join OP.
- Bisect OP, let M’ be the mid-point of OP. Taking M’ as centre and OM’ as radius draw a circle dotted which cuts the inner circle at M and P’.
- Join PM and PP’. Thus, PM and PP’ are the required tangents.
- On measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation:
In right angle ∆OMP,
∠PMO = 90°
PM2 = OP2 – OM2 ...[By Pythagoras theorem i.e. (hypotenuse)2 = (base)2 + (perpendicular)2]
⇒ PM2 = (5)2 – (3)2
= 25 – 9
= 16
⇒ PM = 4 cm
Hence, the length of both tangents is 4 cm.
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.Steps
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°,
find the value of x, y and z.

In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Draw two circles of radii 3.5 cm and 2 cm respectively so that their centres are 6 cm apart. Draw direct common tangents to the circle and show that they are equal in length.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
Draw an isosceles triangle with sides 6 cm, 4 cm, and 6 cm. Construct the incircle of the triangle. Also, write the steps of construction.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
