Advertisements
Advertisements
प्रश्न
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
उत्तर
Given, two concentric circles of radii 3 cm and 5 cm with centre O. We have to draw pair of tangents from point P on outer circle to the other.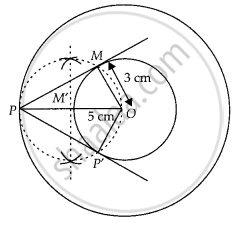
Steps of construction:
- Draw two concentric circles with centre O and radii 3 cm and 5 cm.
- Taking any point P on outer circle. Join OP.
- Bisect OP, let M’ be the mid-point of OP. Taking M’ as centre and OM’ as radius draw a circle dotted which cuts the inner circle at M and P’.
- Join PM and PP’. Thus, PM and PP’ are the required tangents.
- On measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation:
In right angle ∆OMP,
∠PMO = 90°
PM2 = OP2 – OM2 ...[By Pythagoras theorem i.e. (hypotenuse)2 = (base)2 + (perpendicular)2]
⇒ PM2 = (5)2 – (3)2
= 25 – 9
= 16
⇒ PM = 4 cm
Hence, the length of both tangents is 4 cm.
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
The bisectors of angles A and B of a scalene triangle ABC meet at O.
- What is the point O called?
- OR and OQ are drawn perpendicular to AB and CA respectively. What is the relation between OR and OQ?
- What is the relation between angle ACO and angle BCO?
Draw a circle circumscribing a regular hexagon with side 5 cm.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Draw two circles of radii 2.5 cm and 3.5 cm respectively so that their centres are 8 cm apart. Draw direct comm on tangents to the circle.
Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC = 120° and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write down the radius of the circle.
