Advertisements
Advertisements
Question
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Solution
Given, two concentric circles of radii 3 cm and 5 cm with centre O. We have to draw pair of tangents from point P on outer circle to the other.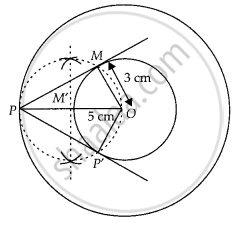
Steps of construction:
- Draw two concentric circles with centre O and radii 3 cm and 5 cm.
- Taking any point P on outer circle. Join OP.
- Bisect OP, let M’ be the mid-point of OP. Taking M’ as centre and OM’ as radius draw a circle dotted which cuts the inner circle at M and P’.
- Join PM and PP’. Thus, PM and PP’ are the required tangents.
- On measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation:
In right angle ∆OMP,
∠PMO = 90°
PM2 = OP2 – OM2 ...[By Pythagoras theorem i.e. (hypotenuse)2 = (base)2 + (perpendicular)2]
⇒ PM2 = (5)2 – (3)2
= 25 – 9
= 16
⇒ PM = 4 cm
Hence, the length of both tangents is 4 cm.
APPEARS IN
RELATED QUESTIONS
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

- Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
- Find its in centre and mark it I.
- With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle. What is the length of the radius of this circle.
Construct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
Draw a circle circumscribing a regular hexagon with side 5 cm.
Draw a line segment AB of length 8 cm. Taking A as centre , draw a circle of radius 4 cm and taking B as centre , draw another circle of radius 3 cm. Construct tangents to each circle form the centre of the other circle.
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
Draw an isosceles triangle with sides 6 cm, 4 cm, and 6 cm. Construct the incircle of the triangle. Also, write the steps of construction.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
