Advertisements
Advertisements
Question
- Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
- Find its in centre and mark it I.
- With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle. What is the length of the radius of this circle.
Solution
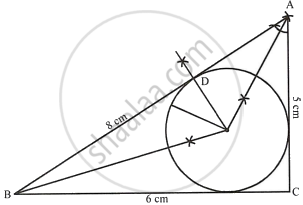
Steps of construction:
- Draw a line segment BC = 6 cm.
- With centre B and radius 8 cm draw an arc.
- With centre C and radius 5 cm draw another arc which intersects the first arc at A.
- Join AB and AC.
ΔABC is the required triangle. - Draw the angle bisectors of ∠B and ∠A intersecting each other at I. Then I is the incentre of the triangle ABC.
- Through I, draw ID ⊥ AB.
- Now from D, cut off `DP = DQ = 2/2 = 1 cm`.
- With centre I and radius IP or IQ, draw a circle which will intersect each side of triangle ABC cutting chords of 2 cm each.
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents form the point P to the circle
Draw two circles of radii 3 cm and 3.5 cm, their centres being 8 cm apart. Construct a transverse common tangent and measure its length.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at end points of those two radii of the circle, the angle between them should be ______.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
Construct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.
