Advertisements
Advertisements
Question
The bisectors of angles A and B of a scalene triangle ABC meet at O.
- What is the point O called?
- OR and OQ are drawn perpendicular to AB and CA respectively. What is the relation between OR and OQ?
- What is the relation between angle ACO and angle BCO?
Solution
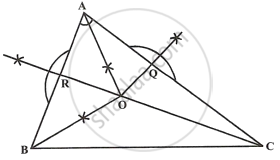
- O is called the incentre of the incircle of ΔABC.
- OR and OQ are the radii of the incircle and OR = OQ.
- OC is the bisector of angle C.
∴ ∠ACO = ∠BCO
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°,
find the value of x, y and z.

In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw two circles of radii 2.5 cm and 3.5 cm respectively so that their centres are 8 cm apart. Draw direct comm on tangents to the circle.
Draw two circles of radii 3 cm and 3.5 cm, their centres being 8 cm apart. Construct a transverse common tangent and measure its length.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
Which of the following is not true for a point P on the circle?
