Advertisements
Advertisements
Question
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Solution
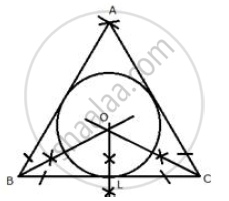
Steps of construction:
- Draw a line segment BC = 5.6 cm
- With centers B and C, draw two arcs of 5.6 cm radius each which intersect each other at A.
- Join AB and AC.
- Draw angle bisectors of ∠B and ∠C intersecting each other at O.
- From O, draw OL ⊥ BC.
- Now with centre O and radius OL, draw a circle which will touch the sides of ΔABC.
This is the required circle.
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
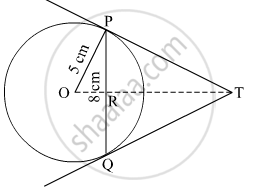
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60º. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
Draw a circle of radius 2.5 cm. Construct a pair of tangents from a point Pat a distance of 6 cm from the centre of the circle.
Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC = 120° and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write down the radius of the circle.
