Advertisements
Advertisements
Question
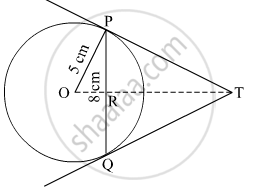
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Solution
PT = TQ (Tangents drawn from a common point to the circle are equal)
So, ΔTPQ is isosceles with PT = TQ and TO is thus the angle bisector of ∠PTQ.
So, OT ⊥⊥ PQ and thus, OT bisects PQ. (Perpendicular drawn from the center of the circle to the chord bisects the chord)
Thus, PR = RQ = 4 cm
Also, in ΔOPR,
OR =`sqrt("OP"^2-"PR"^2)`
`=sqrt(5^2 - 4^2)`
= 3 cm
In ΔTPR,
TR2 + PR2 = TP2
⇒ TR2 + 42 = TP2
⇒ TR2 + 16 = TP2
Let TP = x and TR = y
⇒ Y2 + 16 = X2 .....(1)
In Δ OPT,
TP2 + OP2 = OT2
⇒ TP2 + 52 = (TR + 3)2
⇒ X2 + 25 = (Y + 3)2.................(2)
Using (1) and (2) we get
y =`16/3`
putting this value of y in (1) we get
`(16/3)^2 + 16 = "x"^2`
⇒ `256/9 + 16 = "x"^2`
⇒ `(256+144)/9 ="x"^2`
⇒ `400/9 = "x"^2`
⇒ `"x" = 20/3`
Thus, the length of TP =`20/3`
APPEARS IN
RELATED QUESTIONS
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Draw a circle circumscribing a regular hexagon with side 5 cm.
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°.
Draw an isosceles triangle with sides 6 cm, 4 cm, and 6 cm. Construct the incircle of the triangle. Also, write the steps of construction.
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
Which of the following is not true for a point P on the circle?
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC = 120° and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write down the radius of the circle.
