Advertisements
Advertisements
Question
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
Solution
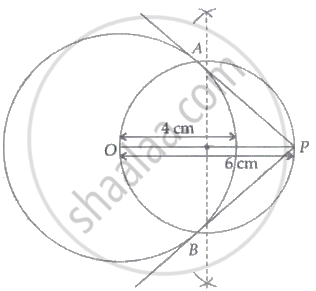
Steps of Construction:
- Construct a circle of radius 4 cm.
- Take a point P, 6 cm away from the centre of the circle.
- Join OP.
- Draw a perpendicular bisector of OM which intersects OP at M.
- Taking M as a centre and OM as the radius, draw another circle which intersects the previous circle at A and B.
- Join PA and PB. PA and PB are the required tangents.
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45°.
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Construct a tangent to a circle of radius 4 cm form a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Draw two circles of radii 2.5 cm and 3.5 cm respectively so that their centres are 8 cm apart. Draw direct comm on tangents to the circle.
Draw two circles with radii 2.5 cm and 4 cm and with their centres 7 cm apart.
Draw a direct common tangent and a transverse common tangent. Calculate the length of the direct common tangent.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60º. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
Construct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.
