Advertisements
Advertisements
Question
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Solution
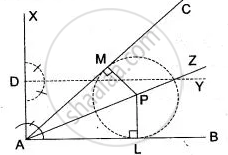
Steps of Construction:
(i) Draw a line AX perpendicular to AB.
(ii) Mark off a point D on AX such that AD = 3.5 cm.
(iii) At D, draw the line DY at right angles to AX. Then DY is the required locus of the centre of circle that touches AB and has a radius of 3.5 cm.
(iv) Construct the bisector AZ of ∠ BAC intersecting DY at P.
(v) Draw PL, PM perpendicular to AB and AC respectively.
(vi) With P as centre and radius equal to 3.5, draw the circle which will pass through L and M.
Then this is the required circle that touches both AB and AC, and whose centre lies within the ∠ BAC.
APPEARS IN
RELATED QUESTIONS
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw a line segment AB of length 8 cm. Taking A as centre , draw a circle of radius 4 cm and taking B as centre , draw another circle of radius 3 cm. Construct tangents to each circle form the centre of the other circle.
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Draw a circle of radius 3 cm. Construct a square about the circle.
Draw an isosceles triangle with sides 6 cm, 4 cm, and 6 cm. Construct the incircle of the triangle. Also, write the steps of construction.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
A pair of tangents can be constructed to a circle inclined at an angle of 170°.
