Advertisements
Advertisements
Questions
Construct a tangent to a circle of radius 4 cm form a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm ?
Solution 1
Steps of Construction
Step 1: Mark a point O on the paper
Step 2: With O as center and radii 4cm and 6cm, draw two concentric circles.
Step 3: Mark a point P on the outer circle.
Step 4: Join OP.
Step 5: Draw the perpendicular bisector XY of OP, cutting OP at Q.
Step 6: Draw a circle with Q as center and radius OQ (or PQ), to intersect the inner circle in points T and T’.
Step 7: Join PT and PT’.

Here, PT and PT’ are the required tangents.
PT = PT’ 4.5 cm (Approx)
Verification by actual calculation
Join OT to form a right ΔOTP (Radius is perpendicular to the tangent at the point of contact)
In right ΔOTP,
` OP^2 =OT^2 + PT^2 ` (Pythagoras Theorem)
`⇒ PT = sqrt(OP^2 - OT^2)`
`⇒PT = sqrt(6^2 -4^2 )= sqrt(36-16) = sqrt(20) ~~ 4.5 cm`
(OP = 6 cm and OT = 4cm)
Solution 2

Steps of construction:
1. Draw two concentric circles with centre O and radii 4 cm and 6 cm. Take a point P on the outer circle and then join OP.
2. Draw the perpendicular bisector of OP. Let the bisector intersects OP at M.
3. With M as the centre and OM as the radius, draw a circle. Let it intersect the inner circle at A and B.
4. Join PA and PB. Therefore, `\overline(PA)` and `\overline(PB)`are the required tangents.
RELATED QUESTIONS
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circles. Give the justification of the construction.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q ?
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
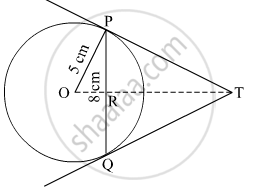
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
