Question

Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circles. Give the justification of the construction.

Answer 1

The required tangents can be constructed on the given circle as follows.

Step 1

Draw a circle with the help of a bangle.

Step 2

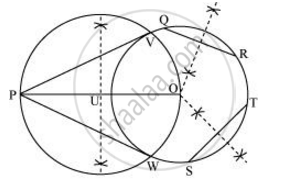
Take a point P outside this circle and take two chords QR and ST.

Step 3

Draw perpendicular bisectors of these chords. Let them intersect each other at point O.

Step 4

Join PO and bisect it. Let U be the mid-point of PO. Taking U as centre, draw a circle of radius OU, which will intersect the circle at V and W. Join PV and PW.

PV and PW are the required tangents.

Justification

The construction can be justified by proving that PV and PW are the tangents to the circle. For this, first of all, it has to be proved that O is the centre of the circle. Let us join OV and OW

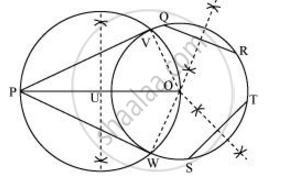
We know that perpendicular bisector of a chord passes through the centre. Therefore, the perpendicular bisector of chords QR and ST pass through the centre. It is clear that the intersection point of these perpendicular bisectors is the centre of the circle. ∠PVO is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.

∴ ∠PVO = 90°

⇒ OV ⊥ PV

Since OV is the radius of the circle, PV has to be a tangent of the circle. Similarly, PW is a tangent of the circle.