Advertisements
Advertisements
प्रश्न
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circles. Give the justification of the construction.
उत्तर
The required tangents can be constructed on the given circle as follows.
Step 1
Draw a circle with the help of a bangle.
Step 2
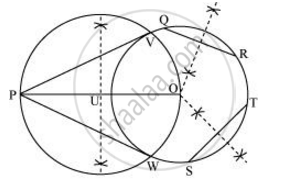
Take a point P outside this circle and take two chords QR and ST.
Step 3
Draw perpendicular bisectors of these chords. Let them intersect each other at point O.
Step 4
Join PO and bisect it. Let U be the mid-point of PO. Taking U as centre, draw a circle of radius OU, which will intersect the circle at V and W. Join PV and PW.
PV and PW are the required tangents.
Justification
The construction can be justified by proving that PV and PW are the tangents to the circle. For this, first of all, it has to be proved that O is the centre of the circle. Let us join OV and OW
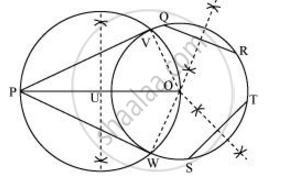
We know that perpendicular bisector of a chord passes through the centre. Therefore, the perpendicular bisector of chords QR and ST pass through the centre. It is clear that the intersection point of these perpendicular bisectors is the centre of the circle. ∠PVO is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠PVO = 90°
⇒ OV ⊥ PV
Since OV is the radius of the circle, PV has to be a tangent of the circle. Similarly, PW is a tangent of the circle.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 3 cm. Take a point at a distance of 5.5 cm from the centre of the circle. From point P, draw two tangents to the circle.
Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Construct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
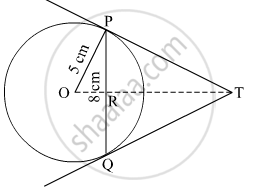
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
A pair of tangents can be constructed from a point P to a circle of radius 3.5cm situated at a distance of ______ from the centre.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.
Construct a pair of tangents to a circle of radius 4 cm from a point P lying outside the circle at a distance of 6 cm from the centre.
