Advertisements
Advertisements
प्रश्न
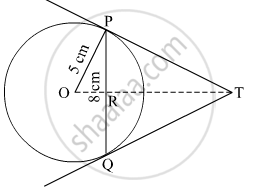
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
उत्तर
PT = TQ (Tangents drawn from a common point to the circle are equal)
So, ΔTPQ is isosceles with PT = TQ and TO is thus the angle bisector of ∠PTQ.
So, OT ⊥⊥ PQ and thus, OT bisects PQ. (Perpendicular drawn from the center of the circle to the chord bisects the chord)
Thus, PR = RQ = 4 cm
Also, in ΔOPR,
OR =`sqrt("OP"^2-"PR"^2)`
`=sqrt(5^2 - 4^2)`
= 3 cm
In ΔTPR,
TR2 + PR2 = TP2
⇒ TR2 + 42 = TP2
⇒ TR2 + 16 = TP2
Let TP = x and TR = y
⇒ Y2 + 16 = X2 .....(1)
In Δ OPT,
TP2 + OP2 = OT2
⇒ TP2 + 52 = (TR + 3)2
⇒ X2 + 25 = (Y + 3)2.................(2)
Using (1) and (2) we get
y =`16/3`
putting this value of y in (1) we get
`(16/3)^2 + 16 = "x"^2`
⇒ `256/9 + 16 = "x"^2`
⇒ `(256+144)/9 ="x"^2`
⇒ `400/9 = "x"^2`
⇒ `"x" = 20/3`
Thus, the length of TP =`20/3`
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circles. Give the justification of the construction.
In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
1) AB.
2) the length of tangent PT.

Draw a line segment AB of length 8 cm. Taking A as centre , draw a circle of radius 4 cm and taking B as centre , draw another circle of radius 3 cm. Construct tangents to each circle form the centre of the other circle.
Draw a circle of radius 3 cm. Construct a square about the circle.
Draw a circle of radius 4 cm. Take a point P outside the circle without using the center at the circle. Draw two tangents to the circle from point P.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
Draw a circle of radius 2.5 cm. Construct a pair of tangents from a point Pat a distance of 6 cm from the centre of the circle.
