Advertisements
Advertisements
प्रश्न
Draw a circle of radius 2.5 cm. Construct a pair of tangents from a point Pat a distance of 6 cm from the centre of the circle.
उत्तर
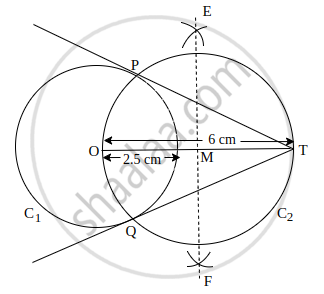
Step of Construction:
- Draw a line segment OT = 6 cm.
- Draw a circle of radius 2.5 cm taking O as centre.
- Draw a perpendicular bisector EF of OT which meets OT at M.
- Taking MT as radius and M as centre, draw a circle C2 which intersects C1 at Pand Q.
- Join TP and TQ.
Hence, TP and TQ are the required tangents.
APPEARS IN
संबंधित प्रश्न
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circles. Give the justification of the construction.
Draw a circle of diameter 9 cm. Mark a point at a distance of 7.5 cm from the centre of the circle. Draw tangents to the given circle from this exterior point. Measure the length of each tangent.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw two tangents to a circle of radius 3.5 cm form a point P at a distance of 6.2 cm form its centre.
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30° with a line passing through the centre.
Construct a tangent to a circle of radius 4 cm form a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Draw two circles of radii 3 cm and 3.5 cm, their centres being 8 cm apart. Construct a transverse common tangent and measure its length.
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
Take a point O on the plane at the paper. With O as center draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.
Draw a circle of radius 3 cm. Construct a square about the circle.
