Advertisements
Advertisements
प्रश्न
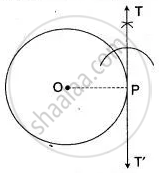
Take a point O on the plane at the paper. With O as center draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.
उत्तर
Steps of construction:
(i) Take a point O on the plane at the paper and draw a circle at radius 3 cm.
(ii) Take a point P on the circle and join OP.
(iii) Construction ∠ OPT = 90°
(iv) Produce TP to T' obtain the required tangent TPT'.
APPEARS IN
संबंधित प्रश्न
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Draw two tangents to a circle of radius 3.5 cm form a point P at a distance of 6.2 cm form its centre.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents form the point P to the circle
Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°.
Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
Draw a circle at a radius of 4 cm. Take a point on it. Without using the centre at the circle, draw a tangent to the circle at point P.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
