Advertisements
Advertisements
Question
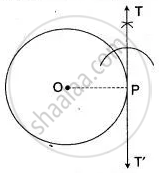
Take a point O on the plane at the paper. With O as center draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.
Solution
Steps of construction:
(i) Take a point O on the plane at the paper and draw a circle at radius 3 cm.
(ii) Take a point P on the circle and join OP.
(iii) Construction ∠ OPT = 90°
(iv) Produce TP to T' obtain the required tangent TPT'.
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 3 cm. Take a point at a distance of 5.5 cm from the centre of the circle. From point P, draw two tangents to the circle.
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the centre of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.
Using ruler and compasses only construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and perpendicular from A on BC is 2.5 cm. Draw a circle circumscribing the triangle ABC and measure its radius.
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Draw a circle of radius 4 cm and take a point Pon its circumference. Construct a tangent to the circle at P.
Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
Draw two circles of radii 2.5 cm and 3.5 cm respectively so that their centres are 8 cm apart. Draw direct comm on tangents to the circle.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
