Advertisements
Advertisements
Question
Draw two circles of radii 2.5 cm and 3.5 cm respectively so that their centres are 8 cm apart. Draw direct comm on tangents to the circle.
Solution
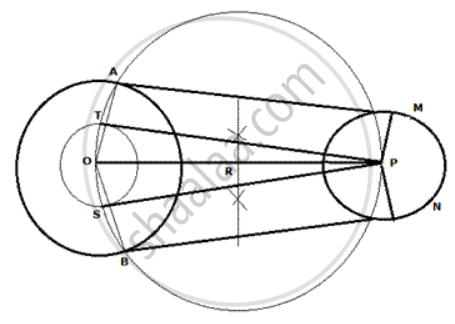
Steps of construction:
(i) Draw a line OP= 8 cm.
(ii) At O, draw a circle of radius 3.5 cm.
(iii) At P, draw a circle of radius 2.5 cm.
(iv) At O, draw a third circle concentric to the bigger circle
and radius = (3.5 - 2.5) cm= 1 cm
(v) Draw a perpendicular bisector of OP. Let R be the mid-point of OP.
(vi) With R as centre and OR as radii, draw a fourth circle. Mark as T and S where the third and fourth circles intersect each other.
(vii) Join OT and OS and extend lines to meet the bigger circle at A and B.
(viii) Join PT and PS.
(ix) On PT and PS, draw perpendiculars to meet the smaller cirde at Mand N.
(x) Join AM and BN.
AM and BN are the required tangents.
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Draw a circle circumscribing a regular hexagon with side 5 cm.
Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw two tangents to a circle of radius 3.5 cm form a point P at a distance of 6.2 cm form its centre.
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q ?
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
