Advertisements
Advertisements
Question
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q ?
Solution
Follow the given steps to draw the tangents to the circles from the two points P and Q:
Step 1. Draw a circle with centre O and radius 3 cm.
Step 2. Extend its diameter on both sides and mark two points P and Q on it such that OP = OQ = 7 cm.
Step 3. Draw the perpendicular bisectors of OP and OQ. Let R and S be the mid-points of OP and OQ, respectively.
Step 4. Draw a circle with R as centre and radius PR, to intersect the circle with centre O at the points T and T'.
Step 5. Draw another circle with S as centre and radius SQ, to intersect the circle with centre O at the points B and B'.
Step 6. Join PT and PT'. Also, join QB and QB'.
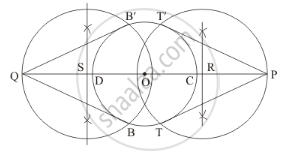
Here, PT and PT' are the tangents to the circle from P. Also, QB and QB' are the tangents to the circle from Q.
APPEARS IN
RELATED QUESTIONS
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
The bisectors of angles A and B of a scalene triangle ABC meet at O.
- What is the point O called?
- OR and OQ are drawn perpendicular to AB and CA respectively. What is the relation between OR and OQ?
- What is the relation between angle ACO and angle BCO?
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60° .
Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ ABC = 60°, and AB 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ ABC of Δ ABC.
There is a circle with center O. P is a point from where only one tangent can be drawn to this circle. What can we say about P?
A pair of tangents can be constructed to a circle inclined at an angle of 170°.
