Advertisements
Advertisements
Question
Draw a circle of radius 4.5 cm. Draw two tangents to this circle so that the angle between the tangents is 60°.
Solution
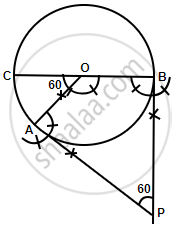
Steps of construction:
- Draw a circle with centre O and radius BC = 4.5 cm.
- Draw arcs making an angle of 180° – 60° = 120° at O such that ∠AOB = 120°.
- At A and B, draw two rays making an angle of 90° at each point which meet each other at point P, outside the circle.
- AP and BP are the required tangents which make an angle of 60º with each other at P.
APPEARS IN
RELATED QUESTIONS
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length.
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw two circles of radii 3.5 cm and 2 cm respectively so that their centres are 6 cm apart. Draw direct common tangents to the circle and show that they are equal in length.
Draw two lines AB, AC so that ∠ BAC = 40°:
(i) Construct the locus of the center of a circle that touches AB and has a radius of 3.5 cm.
(ii) Construct a circle of radius 35 cm, that touches both AB and AC, and whose center lies within the ∠ BAC.
You are given a circle with radius ‘r’ and center O. You are asked to draw a pair of tangents which are inclined at an angle of 60° with each other. Refer to the figure and select the option which would lead us to the required construction. d is the distance OE.

Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60º. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
