Advertisements
Advertisements
Question
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
Solution 1
In order to draw the pair of tangents, we follow the following steps.
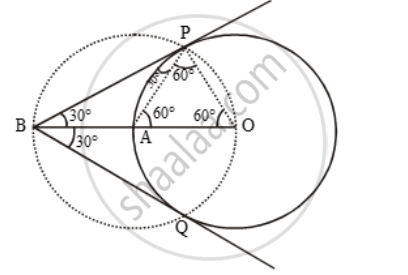
Step I: Take a point O on the plane of the paper and draw a circle of radius OA = 5 cm.
Step II: Produce OA to B such that OA = AB = 5 cm.
Step III: Taking A as the centre draw a circle of radius AO = AB = 5 cm.
Suppose it cuts the circle drawn in step I at P and Q.
Step IV: Join BP and BQ to get the desired tangents.
Justification: In OAP, we have
OA = OP = 5 cm (= Radius) Also,
AP = 5 cm (= Radius of circle with centre A)
∴ ∆OAP is equilateral.
⇒ ∠PAO = 60º ⇒ ∠BAP = 120º
In ∆BAP, we have
BA = AP and ∠BAP = 120º
∴ ∠ABP = ∠APB = 30º ⇒ ∠PBQ = 60º
Solution 2
The tangents can be constructed in the following manner:
Step 1
Draw a circle of radius 5 cm and with centre as O.
Step 2
Take a point A on the circumference of the circle and join OA. Draw a perpendicular to OA at point A.
Step 3
Draw a radius OB, making an angle of 120° (180° − 60°) with OA.
Step 4
Draw a perpendicular to OB at point B. Let both the perpendiculars intersect at point P. PA and PB are the required tangents at an angle of 60°.
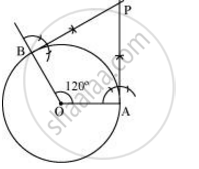
Justification
The construction can be justified by proving that ∠APB = 60°
By our construction
∠OAP = 90°
∠OBP = 90°
And ∠AOB = 120°
We know that the sum of all interior angles of a quadrilateral = 360°
∠OAP + ∠AOB + ∠OBP + ∠APB = 360°
90° + 120° + 90° + ∠APB = 360°
∠APB = 60°
This justifies the construction.
RELATED QUESTIONS
Draw a circle of radius 3 cm. Draw a pair of tangents to this circle, which are inclined to each other at an angle of 60º.
In the given figure PQ is a tangent to the circle at A, AB and AD are bisectors of `angleCAQ` and `angle PAC`. if `angleBAQ = 30^@. prove that:
1) BD is a diameter of the circle
2) ABC is an isosceles triangle

Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents form the point P to the circle
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q ?
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Draw a circle with centre O and radius 3 cm. Take a point P outside the circle. Draw tangents to the circle from P without using the centre and using only ruler and compasses.
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 35°. It is required to draw tangents at the end points of those two radii of the circle, the angle between which is ______.
A circle of radius r has a center O. What is first step to construct a tangent from a generic point P which is at a distance r from O?
